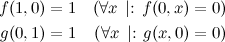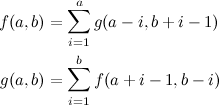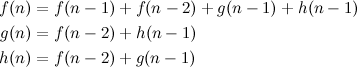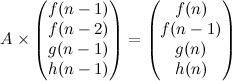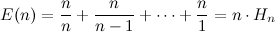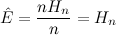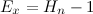Problem Name: Jogging Trails
UVa ID: 10296
LightOJ ID: 1086
Keywords: graph, dynamic programming, eulerian cycle, floyd-warshall, bitmask calculations, chinese postman
In the world of competitive programming, it is very common to come across problems that place the focus on just one or two main algorithmic concepts, such that you can more or less solve them by simply following a “standard” recipe, or by doing a few simple variations over the classic algorithms. However, not every problem is like that.
There are problems that involve several different concepts, and their algorithmic elements intertwine in interesting and elegant ways to create a new type of challenge. A challenge that provides great satisfaction and a powerful sense of fulfillment once you find out a valid way to rearrange and mix the ingredients from different recipes to create your own solution. Moreover, from my own limited experience observing the work of some of the greatest competitive programmers on the planet, it is my belief that perhaps the main difference between them (the really, really good algorithm problem solvers), and the average programmers —beyond the obvious things, like the amount of experience and knowledge—, is their deep understanding of the “recipes” and their creativity to mix them in order to solve a new complex problem.
Jogging Trails, the problem I’ll talk about here, is a relatively “simple” problem, but it’s a very nice example of this type of beautiful “intertwining” of different concepts. It’s easy to summarise the problem like this: you receive a weighted, undirected and connected graph; you have to find the “cost” of the shortest route that starts and ends on the same vertex after visiting every edge at least once. This is also known as the Chinese postman problem, or the route inspection problem.
There are many interesting things to talk about in this problem, so we’ll approach them gradually. Let’s start with an example to help us illustrate our ideas down the road. Consider the following graph:
Okay, first things first. Try to manually find the solution for this example. Finding it quickly is not very easy. One of the first things you’ll probably notice is that it’s tricky to find a route that starts and ends on the same node, after having visited each edge exactly once. In fact, it’s impossible.
This is where the first interesting algorithmic idea comes to play, and it is that of an Eulerian cycle or circuit. It simply refers to a cycle inside a graph that visits each edge exactly once. What is useful to remember is this (quoting from Wikipedia):
An undirected graph has an Eulerian cycle if and only if every vertex has even degree, and all of its vertices with nonzero degree belong to a single connected component.
In other words, assuming you have a connected graph (like in our case), count the number of edges connected to each node and if every node has an even number of them, then you absolutely can do a tour that starts and ends on the same place, and visits all edges exactly once. This means that if our example showed that property (every node had an even degree), then we would not have to do anything special, the answer would just be the sum of weights of all edges. Simple, right? Remember that we don’t need to calculate the path itself, just its cost.
However, we aren’t that lucky in our example. We have five nodes, and four of them have an odd degree. What this implies is that whatever shortest path there might exist in there, it must visit some edges more than once, there’s no other way around it. The question is, obviously, which edges will we have to visit twice or more? Actually, we don’t really need to know which edges, just how much additional cost will they represent for our final answer.
At this point, it could be useful to apply a general strategy that is usually seen in graph–related problems. If you know of a certain algorithm or idea that can help you but it can’t be applied to your graph directly, try modifying your graph until it does! This is a common technique used, for example, when you want to calculate things like the max flow in a network and so you invent “dummy” nodes and edges in order to apply the algorithm properly.
In this case, what if we think about “dummy” edges that can turn all nodes into even–degree nodes? Something like this:
There are many possible ways in which these fake edges could be created to make this graph favourable for finding an Eulerian cycle. We could, for example, connect nodes \((2, 3)\) and \((1, 4)\), or we could do \((2, 1)\) and \((3, 4)\), and for each of these connections there are many ways to do it as well. For instance, for the fake edge \((2, 3)\) there are many ways to go from 2 to 3, like going directly (with a cost of 25), or going through node 1 (with a cost of 23). It is important to keep in mind that the fake edges are just something to help us model the graph as something where you can actually find an Eulerian tour, but they just represent paths that exist over the real edges.
In any case, what we’re interested in is a combination of fake edges that provide the minimal additional cost. So we arrive to the second algorithmic idea to be applied in this problem. In order to try the different available combinations that can form our fake edges, it is in our best interest to find out the shortest paths between all pairs of nodes, and since the number of nodes in the graph is very low (\(n \leq 15\)), the Floyd-Warshall algorithm fits the bill perfectly.
After this step, we would end up with the following information:
A little examination should reveal that the best possible combination of fake edges among the nodes \((1, 2, 3, 4)\) would be from the shortest paths between \((1, 2)\) and \((3, 4)\). Our extended graph would then look like this:
Try finding the solution now. Doing an Eulerian tour is now a breeze, and it is pretty evident that the edges that have to be visited twice are \((2, 1)\), \((4, 5)\) and \((3, 5)\). The final answer for this example is 109, the sum of all edges in this extended graph.
We are getting close, but we still haven’t figured out just exactly how are we going to find the best combination of fake edges. This is where the third and final algorithmic concept comes in: dynamic programming, with a little bit of bitwise manipulations.
Again, because the number of nodes is small, it is feasible to formulate the following D.P. relation:
- \(f(S)\)
- The minimum cost of connecting pairs of nodes among the set \(S\) (represented as a bitmask in code).
This relation is very simple: the base case is an empty set of nodes, which has a cost of zero; otherwise we try every pair \(P\) of nodes among the set, and find the sum of the shortest path between the pair of nodes and the value of \(f(S - P)\). We keep the overall minimum of these values.
Let’s see an example of a top–down implementation of this in C++:
#define MAXN 15
#define INF (1 << 30)
#define GetFS(b) ((b) & -(b)) // get first set bit
#define ClrFS(b) (b &= ~GetFS(b)) // clear first set bit
static const int m37pos[] = {
32, 0, 1, 26, 2, 23, 27, 0, 3,
16, 24, 30, 28, 11, 0, 13, 4, 7,
17, 0, 25, 22, 31, 15, 29, 10, 12,
6, 0, 21, 14, 9, 5, 20, 8, 19, 18
};
#define Ctz(x) (m37pos[(x) % 37]) // count of trailing zeroes
typedef unsigned int u32;
// We assume that this matrix contains the shortest paths among all pairs of
// vertices (i.e. after running Floyd-Warshall)
int g[MAXN][MAXN];
// Memoization structure
int memo[1 << MAXN];
/**
* Minimum cost of increasing by one the degree of the set of vertices given,
* to make them even.
*
* @param b Bitmask that represents the nodes with an odd degree
* @return The minimum cost
*/
int f(u32 b)
{
if (b == 0) return 0;
if (memo[b] >= 0) return memo[b];
int best = INF;
int nv = 0; // number of vertices in the bitmask
int vs[MAXN]; // list of vertices
// populate list of vertices from the bitmask
for (u32 r = b; r; ClrFS(r)) {
u32 x = GetFS(r);
vs[nv++] = Ctz(x);
}
// try all pairs of vertices
for (int i = 0; i < nv; ++i)
for (int j = i + 1; j < nv; ++j) {
u32 p = (1 << vs[i]) | (1 << vs[j]);
int cur = g[ vs[i] ][ vs[j] ] + f(b & ~p);
if (cur < best) best = cur;
}
return memo[b] = best;
}
There are a few interesting things in here for you to analyse if you haven’t done this kind of “bitwise” D.P. before, but they are very accessible once you are familiar with bitwise manipulations. The code from lines 4–13 just provides a few useful macros to deal with bits —the code for Ctz comes from Bit Twiddling Hacks, a very useful resource for you to explore, if you haven’t done so already.
There are two external data structures (lines 21 and 24) that we depend on, and then the D.P. function itself is defined on line 34. In order to call this function you need to fill the memo array with the value -1, and then pass the bitmask of all vertices with odd degree as a parameter. The value returned by f plus the sum of all edges in the original graph provide the final answer.
And now we have reached the end. We took elements from different algorithmic areas (graph theory, cycles, shortest paths, dynamic programming, bitwise calculations) to solve the Chinese postman problem. Wasn’t it fun?