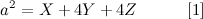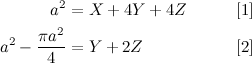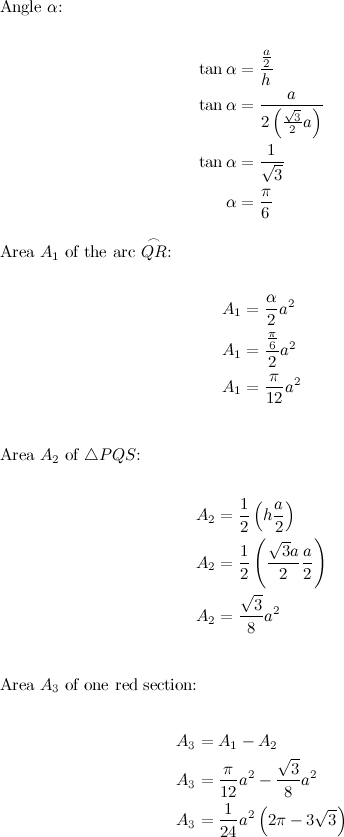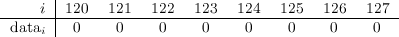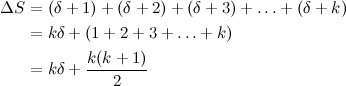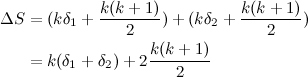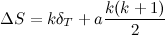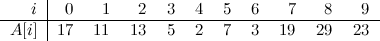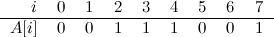Problem Name: Ahoy, Pirates!
UVa ID: 11402
Keywords: segment tree, lazy propagation
Working on algorithm problems has been one of my favourite hobbies for a while now, and I’m constantly inspired by the fact that, although there is a finite (and not too large) set of concepts that cover the landscape of all possible problems you can encounter, in practise it feels like there are no boundaries to the amount of things you can learn. In a very real sense, you can always keep learning new things, and the more you learn, the more you find new things that you want to learn next.
I still have many gaps in some basic areas, so I like diving into new things whenever I have the chance to do it. For example, it’s only recently that I have learned a little about a few data structures that were a mystery to me for a long time; segment trees, binary indexed trees, sparse tables, k-d trees… For this reason, I think the next few entries I’ll write for this blog will be for problems related to these data structures. I’ll start with the segment tree by having a crack at this problem —Ahoy, Pirates!— which I think is a very nice exercise for developing a deeper understanding of a ST and the subtleties of implementing update operations on it.
The Problem
Consider a large array of boolean values, represented as zeroes and ones. You have to implement four types of operations that can be performed over this array:
- Set, or “turn on” a range of adjacent positions in the array (set them to 1).
- Clear, or “turn off” a range (set to 0).
- Flip a range (turn zeroes into ones and vice–versa).
- Query the number of ones in a given range.
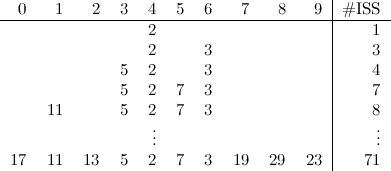
Very interesting problem, if you ask me. We’ll begin with a simple example, as usual. Let’s say we start with an array \(A\) of size 8, and with the following contents:
Querying, First Approach
Now, let’s say we receive a query that asks for the number of ones in a range \([i:j]\) with \(0 \leq i \leq j < N\), where \(N\) is the size of the array (8 in this example). One simple idea is to simply traverse the array with a loop from \(i\) to \(j\), counting the number of ones in the way.
That would be an acceptable solution if that were the only query to answer, or if the number of queries were very low. However, given that the array is big, and there’s a relatively large number of queries, a complexity of \(O(NQ)\) is too high for our needs.
What we’ll do instead is use a segment tree. This is a very nice data structure where a binary tree (typically a binary heap) is built on top of an array in order to store useful information from the underlying data in groups of increasing size. The leaves of the tree correspond to the individual positions inside the array, while internal nodes represent data that is the result of combining information from its children. The root corresponds to an interval that encloses the whole array.
Let’s try to visualise this with our example:
This graph depicts three things for each node in the tree: its interval (enclosed in a purple box), its index (in red) and its contents (in blue), which in this example corresponds to the number of ones in the corresponding interval. Note the convenient way in which the indices of all nodes are related to each other, as is common in heap–like data structures. In this case, the convention is that for a node \(i\), its two children have indices \(2i\) and \(2i + 1\). As you can see, although this data structure represents a tree, it can be stored in a plain array of size 16 (index zero is left unused).
Now, consider why building something like this is useful. If we receive a query that asks for the number of ones in the whole array, we don’t need to go any further than the root of the tree; in other words, an operation that would have taken us \(N\) steps with a common loop, takes us only a single step now. Similarly, if we’re asked about the range \([0:3]\), we just need to visit two nodes: the root and its left child.
Some queries may involve combining the answer from different paths. For example, if we have a query for the range \([2:6]\) then the following nodes of the tree would have to be visited: 1, 2, 5, 3, 6, 7 and 14. This might seem like a bad trade–off in this small example, but it is a huge gain in general. In fact, it’s easy to see that the complexity for an arbitrary query goes from \(O(N)\) to \(O(\log{N})\).
Updating the Tree
So far so good, but what would happen if we try to update the tree after it has been built? Let’s focus on just the Set operation for now.
For the reasons we have discussed before, we should avoid updating the underlying array and then re–building the whole tree; that would have an excessively high complexity. Instead, we can observe this: since every node is implicitly associated with an interval of the array, it’s easy to find out how many positions it covers, and that way we can easily determine the new contents of each affected node after a Set operation.
Back to our example. Let’s say that we receive a query that asks us to set the range \([1:7]\). This is how it could look like just after the relevant nodes have been updated:
The update process (as any operation performed on a ST) starts with the root. The tree is traversed downwards via recursive calls until a node that is completely contained in the relevant interval is found. Those nodes are then updated first (the nodes with blue background). The changes then propagate upwards, as the recursion stops and the stack is popped back until we’re back at the root again (these changes happen in the nodes with gray background).
In this example we can see how, for example, the path from the root to node 9 seems fine and needs no adjustments. Same thing with the sub-tree at node 5, but only by chance, because the contents of that node didn’t change (the range \([2:3]\) of the array already had two ones). However, notice the resulting situation for node 3. At this point, if we received a query asking for the number of ones in an interval that completely contained the range \([4:7]\), we’d have no trouble to find the answer; the information of the root and node 3 is correct. However, the sub–tree at node 3 is inconsistent. If, for instance, we received a query for the interval \([4:5]\), we’d reach node 6 and find the old value of 1 there, which is not correct.
Lazy Propagation
It has been said —by notoriously bright people— that laziness is one of the three great virtues of programmers. As it turns out, laziness is also a desirable property for algorithms. When we update the tree, we don’t want to always propagate the changes down to the leaves (which would be even worse than just updating the original array of integers in a loop). However, we don’t want to leave the tree in an inconsistent state either.
The solution is to extend the tree with an extra field that indicates whether the relevant sub–tree needs to be updated or not. This way, nodes in the tree are properly updated as needed by future queries, and not a moment before; hence the lazy name.
We will extend our tree, then. Since we have three types of operations that change the tree, we’ll store a flag that stores one of four possible values: S for a set operation, C for a clear operation, F for a flip operation, and N for nothing, meaning that the current node is up–to–date —unless one of its ancestors is not N, but that would be handled in due time. This is how our example would look like after the update, with the extended information (there’s a new state field in green):
This tree, unlike the previous one, has now enough information to maintain a consistent state at all times. Note that now nodes 10, 11, 6 and 7 are marked with S, meaning that the next time they are visited, a Set operation will be propagated (lazily) from them. We could have left nodes 10 and 11 untouched because, as has been mentioned, node 5 didn’t change, but we’ll leave them marked just to illustrate the basic process without special checks.
At this point, let’s say that we received a query asking for the number of ones in the range \([4:5]\). This time node 6 is visited, but since it’s marked S, then first we’d have to propagate the Set operation, which means updating the contents of node 6 itself, and then marking its children so the lazy propagation continues with them if necessary. This continuous propagation of previously marked nodes ensures that the information of the tree is always correct, without updating more nodes than necessary. A very powerful technique.
In order to illustrate the operations we haven’t considered yet, let’s say that we also receive a query to Clear range \([7:7]\), and a query to Flip range \([0:3]\). This is how the tree would look like after all these operations:
Okay, to summarise, this is what we’ve imagined so far in our example:
- Building the tree.
- A Query for range \([0:7]\). The result is 4 and is obtained just by looking at the root.
- Queries for ranges \([0:3]\) and \([2:6]\). They need to visit more nodes of the tree, but the result is still obtained in \(O(\log{N})\).
- A Set operation for the range \([1:7]\). It updates directly nodes 9, 5 and 3, and their ancestors, and marks their children so they are lazily updated in the future.
- A Query for range \([4:5]\). This updates node 6 (because it was marked S), and marks its children for future propagation.
- A Clear operation for range \([7:7]\).
- A Flip operation for range \([0:3]\).
The “array” (which lives now inside our ST) now has a total of four ones, yet this is not clear from looking at the leaves alone. You need to analyse the internal nodes to understand how is it that this array has been modified, and what updates have not been propagated yet.
But wait a minute, did you notice how node 14 has a one now, and its state is N? When did that happen? Then answer is, it happened in the middle of the Clear for \([7:7]\). The sequence of events was like this:
- A Clear for \([7:7]\) was requested.
- The tree is traversed from the root, and it goes recursively down to nodes 3 and 7. At this point it finds that node 7 is marked S.
- It propagates this change, which means changing the contents of node 7 to 2, and marking its children (nodes 14 and 15) with S.
- Immediately after that, it continues with its original request, but to handle it, it has to visit 7’s children first, so it goes down to nodes 14 and 15.
- This is when the changes happen. I had not mentioned this before, but the way the tree is traversed, it needs to keep visiting nodes, until either a node is completely inside the relevant interval (like node 15 here), or it’s completely outside the interval (like node 14 here). So, node 14 is visited, and since it’s marked S, it changes its value to 1, resets its state to N and it stops traversing this branch.
- Node 15 is updated according to the Clear request, and stops there as well.
- All these changes propagate back upwards, resulting in the tree you see in the last figure.
I hope this overview has helped you in case you haven’t worked with segment trees before.
I want to end this by mentioning a curious detail that applies to this specific problem as a result of the operations it involves. Consider the situation of nodes 5, 10 and 11 in the last figure. Node 5 is marked F and its children are marked S. Now consider what would need to happen if, for example, you receive a query for range \([2:3]\). In other words, think about what happens if a node \(u\) with state \(s(u)\) is visited, and one of \(u\)’s children is node \(v\) with state \(s(v)\). How should state \(s(u)\) be propagated down to \(s(v)\)?
There’s a few alternatives:
- If \(s(u)\) is N, then nothing needs to happen.
- If \(s(u)\) is S or C, those operations are overriding, meaning that the state of \(v\) must be set to \(s(u)\) regardless of the previous contents of \(s(v)\).
- However, if \(s(u)\) is F, then the previous contents of \(s(v)\) are important, and they need to change accordingly:
- If \(s(v)\) was N, it becomes F.
- C becomes S.
- S becomes C.
- F becomes N.
Kinda cool, isn’t it?
Sample Code
I usually don’t include source code in my posts because I prefer describing the general algorithms, but in this case I’ll attach the basics of my segment tree code for this problem, because I know that finding reference code for this data structure on the web can be a little difficult.
This code con be simplified much further by combining similar code from different methods, but this way you can see how every individual operation is implemented separately, and it also makes it easy to identify the common patterns of manipulating the segment tree.
#define MAXN 1024000
#define MAXH 21 // 1 + ceil(log2(MAXN))
// Flags to identify states. 0 is for "Nothing".
#define UP_SET 1
#define UP_CLR 2
#define UP_FLP 3
struct SegTree {
vector<int> A; // original array of integers
vector<int> T; // segment tree
vector<int> U; // segment tree for lazy propagation (the states)
int n; // size of the array
SegTree(int N=0) : n(N) {
A.resize(MAXN);
T.resize(1 << MAXH);
U.resize(1 << MAXH);
}
void init() { tree_init(1, 0, n-1); }
void tree_init(int x, int a, int b) {
U[x] = 0;
if (a == b) { T[x] = A[a]; return; }
int lt = 2*x, rt = lt + 1, md = (a+b)/2;
tree_init(lt, a, md);
tree_init(rt, md + 1, b);
T[x] = T[lt] + T[rt];
}
void set(int i, int j) { tree_set(i, j, 1, 0, n - 1); }
void tree_set(int i, int j, int x, int a, int b) {
propagate(x, a, b);
if (j < a || i > b) return;
if (a == b) { T[x] = 1; return; }
int lt = 2*x, rt = lt + 1, md = (a+b)/2;
if (a >= i && b <= j) {
T[x] = b - a + 1;
U[lt] = U[rt] = UP_SET;
return;
}
tree_set(i, j, lt, a, md);
tree_set(i, j, rt, md + 1, b);
T[x] = T[lt] + T[rt];
}
void clear(int i, int j) { tree_clear(i, j, 1, 0, n - 1); }
void tree_clear(int i, int j, int x, int a, int b) {
propagate(x, a, b);
if (j < a || i > b) return;
if (a == b) { T[x] = 0; U[x] = 0; return; }
int lt = 2*x, rt = lt + 1, md = (a+b)/2;
if (a >= i && b <= j) {
T[x] = 0;
U[lt] = U[rt] = UP_CLR;
return;
}
tree_clear(i, j, lt, a, md);
tree_clear(i, j, rt, md + 1, b);
T[x] = T[lt] + T[rt];
}
void flip(int i, int j) { tree_flip(i, j, 1, 0, n - 1); }
void tree_flip(int i, int j, int x, int a, int b) {
propagate(x, a, b);
if (j < a || i > b) return;
if (a == b) {
T[x] = T[x] == 1 ? 0 : 1;
return;
}
int lt = 2*x, rt = lt + 1, md = (a+b)/2;
if (a >= i && b <= j) {
T[x] = (b - a + 1) - T[x];
U[lt] = apply_flip(U[lt]);
U[rt] = apply_flip(U[rt]);
return;
}
tree_flip(i, j, lt, a, md);
tree_flip(i, j, rt, md + 1, b);
T[x] = T[lt] + T[rt];
}
int query(int i, int j) { return tree_query(i, j, 1, 0, n-1); }
int tree_query(int i, int j, int x, int a, int b) {
if (j < a || i > b) return -1;
propagate(x, a, b);
if (a >= i && b <= j) return T[x];
int lt = 2*x, rt = lt + 1, md = (a+b)/2;
int q1 = tree_query(i, j, lt, a, md);
int q2 = tree_query(i, j, rt, md + 1, b);
if (q1 < 0) return q2;
if (q2 < 0) return q1;
return q1 + q2;
}
int apply_flip(int v) {
if (v == UP_SET) return UP_CLR;
if (v == UP_CLR) return UP_SET;
if (v == UP_FLP) return 0;
return UP_FLP;
}
void propagate(int x, int a, int b) {
if (U[x] == 0) return;
if (U[x] == UP_SET)
T[x] = b - a + 1;
else if (U[x] == UP_CLR)
T[x] = 0;
else if (U[x] == UP_FLP)
T[x] = (b - a + 1) - T[x];
if (a != b) {
int lt = 2*x, rt = lt + 1;
if (U[x] == UP_SET || U[x] == UP_CLR)
U[lt] = U[rt] = U[x];
else
U[lt] = apply_flip(U[lt]), U[rt] = apply_flip(U[rt]);
}
U[x] = 0;
}
};